Strengthening Math Fluency Through Cognitive Science
Strengthening Math Fluency Through Cognitive Science
Arithmetic fluency, the efficient, accurate, and relatively effortless recall of basic addition, subtraction, multiplication, and division facts, is one of the strongest predictors of long-term math achievement and overall academic success. However, its role in math education has been widely misunderstood. Some argue that memorizing math facts is harmful or outdated, while others insist on a return to traditional drills. But all concur that the nation’s persistent math underperformance underscores the urgent need to strengthen foundational fluency.
Fact Sheet
School Level - Match proficiency

“Students still haven’t caught up to where they were before COVID-19… Five years after classrooms first shut down, student achievement remains below pre-pandemic levels, especially in math.”
Education Week
At Grade 4:
performed at or above NAEP Proficient in math (2024).
At Grade 8:
performed at or above NAEP Proficient in math (2024).
At Grade 12:
were at or above NAEP Proficient (2024)
scored below NAEP Basic (2024). This is the highest share below Basic ever reported for Grade 12. The Grade-12 average math score is the lowest since NAEP began reporting in 2005.
STEM Readiness

Misconceptions about teaching and learning based on intuition have led to an epidemic of disengagement in schools (Evans, 2023), higher education (Chronicle of Higher Ed, 2022; NY Times, 2022), and the workplace (Society for HR Management, 2023).
Benchmark Unmet
of graduates met all four ACT college-readiness benchmarks (English, Reading, Math, Science) in 2023.
of students met the ACT STEM College Readiness Benchmark in 2023, down from 20 percent in 2018-19
Understanding Math Fluency: A Cognitive Perspective Informed by McNeil et al. (2025)
This framework illustrates how arithmetic fluency is strengthened through the integration of structured practice and conceptual understanding, which McNeil et al. (2025) identify as mutually reinforcing components of fluent mathematical thinking. Structured practice develops automaticity, while conceptual understanding develops flexible strategies, and together they reduce working-memory demands during problem solving. Working memory sits at the center because, as the research emphasizes, students who can retrieve facts efficiently free cognitive resources for higher-level reasoning rather than calculation steps. Executive functions operate across both sides, coordinating attention, regulation, and strategy use, enabling learners to connect prior knowledge with new information and monitor their own thinking as fluency develops.
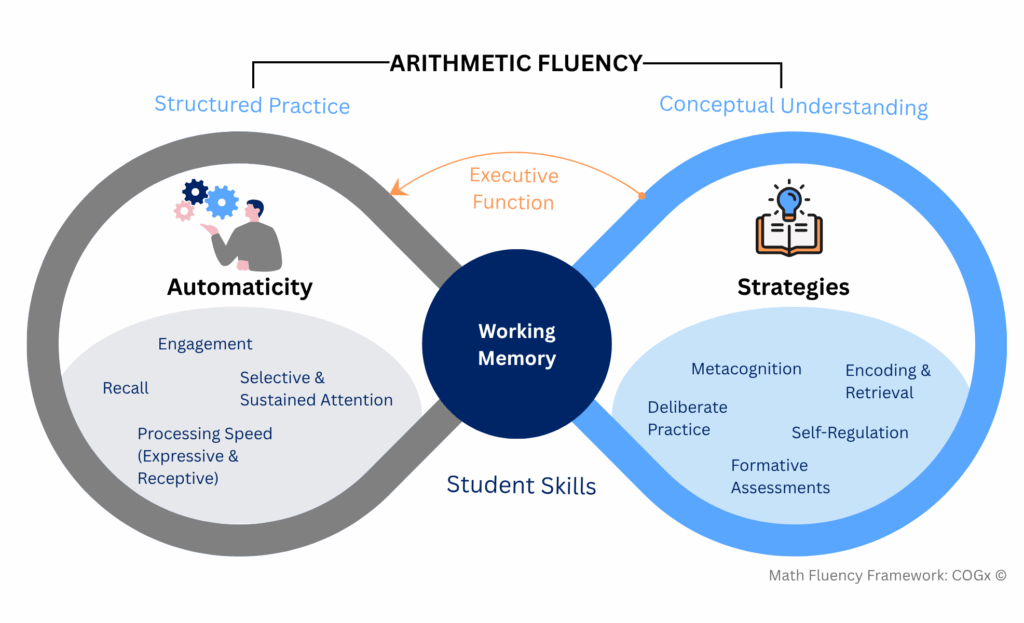
Cognitive Skills Essential for Developing Fluency, And How We Build Them
Engagement:
Educators learn how to foster positive emotions, belonging, and intrinsic motivation, while students learn how emotions and mindset influence their capacity to stay engaged during learning.
Recall:
Educators learn evidence-based retrieval practices to strengthen memory, while students learn to use retrieval and spaced repetition to recall facts more efficiently.
Expressive & Receptive Processing:
Educators learn strategies to improve clarity of instruction and communication, while students learn how to better interpret information and express mathematical reasoning.
Selective Attention:
Educators learn how to capture and direct student focus, while students learn to recognize distractions and refocus their attention during math tasks.
Sustained Attention:
Educators learn methods to support varied processing speeds and maintain classroom focus, while students learn practical tools, such as mindfulness and goal-setting, to sustain effort long enough for automaticity to form.
Metacognition:
Educators learn to teach reflective routines that promote deep learning, while students learn to monitor their thinking, evaluate strategies, and adjust when problem solving becomes challenging.
Self-Regulation:
Educators learn frameworks to support planning, emotional regulation, and follow-through, while students learn how to manage frustration, stay organized, and persist through difficult tasks.
Encoding & Retrieval:
Educators learn how to incorporate chunking, visualization, and retrieval into lesson design, while students learn to use these techniques to encode information deeply and recall it more reliably.
Deliberate Practice:
Educators learn to design purposeful, targeted practice that builds understanding, while students learn how to practice intentionally rather than repeating procedures mindlessly.
Formative Assessment:
Educators learn how to use ongoing assessment to guide instruction and identify misconceptions, while students learn to analyze mistakes and apply feedback to strengthen their strategies and understanding.



